In ∆ABC, ∠ABC = 135°.

We have the following figure.

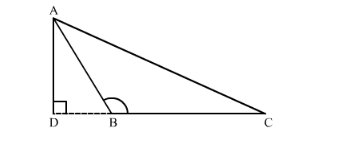
Here $\triangle A D B$ is a right triangle right angled at $D$. Therefore by Pythagoras theorem we have

$A B^{2}=A D^{2}+D B^{2}$

Again $\triangle A D C$ is a right triangle right angled at $D$.

Therefore, by Pythagoras theorem, we have

$A C^{2}=A D^{2}+D C^{2}$

$A C^{2}=A D^{2}+(D B+B C)^{2}$

$A C^{2}=A D^{2}+D B^{2}+B C^{2}+2 . B C . B D$

Since angle $A B D$ is $45^{\circ}$ and therefore angle $B A D$ is also $45^{\circ}$.

Hence AB = DB

So,

$A C^{2}=A D^{2}+D B^{2}+B C^{2}+2 B C \times A D$

$=A D^{2}+D B^{2}+B C^{2}+2 \times 2 \times \frac{1}{2} B C \times A D$

$=A D^{2}+D B^{2}+B C^{2}+4 a r(\Delta A B C)$

Since $A B^{2}=A D^{2}+D B^{2}$

So,

$A C^{2}=A B^{2}+B C^{2}+4 \operatorname{ar}(\triangle A B C)$

Hence we have proved that $A C^{2}=A B^{2}+B C^{2}+4 a r(\triangle A B C)$