In ∆ABC, D and E are the mid-points of AB and AC respectively.

Given: In ΔABC, D and E are the midpoints of AB and AC respectively.

To find: Ratio of the areas of ΔADE and ΔABC.

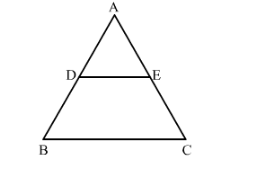
Since it is given that D and E are the midpoints of AB and AC, respectively.

Therefore, DE || BC                   (Converse of mid-point theorem)

Also, DE=12BC

In ΔADE and ΔABC

∠ADE=∠B              Corresponding angles

∠DAE=∠BAC       Common

So, ∆ADE~∆ABC      (AA Similarity)

We know that the ratio of areas of two similar triangles is equal to the ratio of squares of their corresponding sides.

$\frac{\operatorname{ar}(\Delta \mathrm{ADE})}{\operatorname{ar}(\Delta \mathrm{ABC})}=\left(\frac{\mathrm{AD}}{\mathrm{AB}}\right)^{2}$

$\frac{\operatorname{ar}(\Delta \mathrm{ADE})}{\operatorname{ar}(\Delta \mathrm{ABC})}=\left(\frac{1}{2}\right)^{2}$

$\frac{\operatorname{ar}(\Delta \mathrm{ADE})}{\operatorname{ar}(\Delta \mathrm{ABC})}=\left(\frac{1}{4}\right)$