In ∆ABC, DE is drawn parallel to BC, cutting AB and AC at D and E, respectively, such that AB = 7.2 cm
Question:
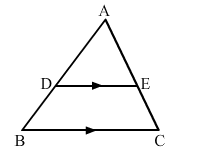
In ∆ABC, DE is drawn parallel to BC, cutting AB and AC at D and E, respectively, such that AB = 7.2 cm, AC = 6.4 cm and AD = 4.5 cm. Find AE.
(a) 5.4 cm
(b) 4 cm
(c) 3.6 cm
(d) 3.2 cm
Solution:
(b) 4 cm
It is given that DE
Applying basic proportionality theorem, we get:
$\frac{A D}{A B}=\frac{A E}{A C}$
$\Rightarrow \frac{4.5}{7.2}=\frac{A E}{6.4}$
$\Rightarrow A E=\frac{4.5 \times 6.4}{7.2}=4 \mathrm{~cm}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
