Question:
In $\triangle \mathrm{ABC}$ (Fig. 4.59), if $\angle 1=\angle 2$, prove that $\mathrm{ABAC}=\mathrm{BDDC}$.
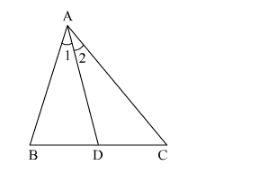
Solution:
We have to prove that $\frac{A B}{A C}=\frac{B D}{D C}$.
In ∆ABC,
$\angle \mathrm{l}=\angle 2$ (Given)
So, $A D$ is the bisector of $\angle A$
Therefore, $\frac{A B}{A C}=\frac{B D}{D C}$