In ∆ABC, ray AD bisects ∠A and intersects BC in D. If BC = a, AC = b and AC = c, prove that

Given: In $\triangle A B C$ ray $A D$ bisects angle $A$ and intersects $B C$ in $D$, If $B C=a, A C=b$ and $A B=c$

To Prove:

(i) $B D=\frac{a c}{b+c}$

(ii) $D C=\frac{a b}{b+c}$

(i) The corresponding figure is as follows

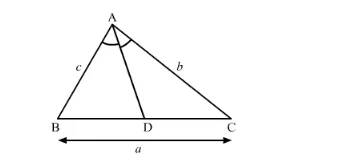
Proof. In triangle $A B C, A D$ is the bisector of $\angle A$

Therefore $\frac{A B}{A C}=\frac{B D}{C D}$

Substitute $B C=a, A C=b$ and $A B=c$ we get,

$\frac{c}{b}=\frac{B D}{B C-B D}$

$\frac{c}{b}=\frac{B D}{a-B D}$

By cross multiplication we get.

$c(a-B D)=b \times B D$

$a c-c B D=b B D$

$a c=b B D+c B D$

$a c=(b+c) B D$

$\frac{a c}{b+c}=B D$

We proved that $B D=\frac{a c}{b+c}$

(ii) Since $B C=C D+B D$

$\Rightarrow C D=B C-B D$

$C D=a-\frac{a c}{b+c}$

$=\frac{a b}{b+c}$