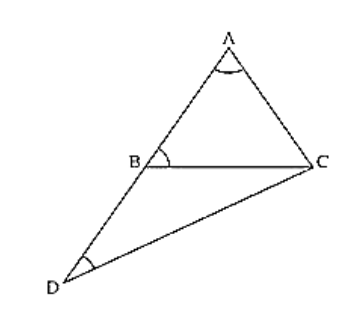
In ΔABC, side AB is produced to D so that BD = BC. If ∠B = 60°

Given that, in Δ ABC, side AB is produced to D so that BD = BC.

∠B = 60°, and ∠A = 70°

To prove,

(i) AD > CD (ii) AD > AC

First join C and D

We know that,

Sum of angles in a triangle =180°

∠A + ∠B + ∠C = 180°

70° + 60° + ∠C = 180°

∠C = 180° - (130°) = 50°

∠C = 50°

∠ACB = 50° ... (i)

And also in Δ BDC

∠DBC =180 - ∠ABC [ABD is a straight angle]

180 - 60° = 120°

and also BD = BC[given]

∠BCD = ∠BDC [Angles opposite to equal sides are equal]

Now,

∠DBC + ∠BCD + ∠BDC = 180° [Sum of angles in a triangle =180°]

⟹ 120° + ∠BCD + ∠BCD = 180°

⟹ 120° + 2∠ BCD = 180°

⟹ 2∠BCD = 180° - 120° = 60°

⟹ ∠BCD = 30°

⟹ ∠BCD = ∠BDC = 30° .... (ii)

Now, consider ΔADC.

∠BAC ⟹ ∠DAC = 70° [given]

∠BDC ⟹ ∠ADC = 30° [From (ii)]

∠ACD = ∠ACB + ∠BCD

= 50° + 30°[From (i) and (ii)] = 80°

Now, ∠ADC < ∠DAC < ∠ACD

AC < DC < AD [Side opposite to greater angle is longer and smaller angle is smaller]

AD > CD and AD > AC

Hence proved

Or,

We have,

∠ACD > ∠DAC and ∠ACD > ∠ADC

AD > DC and AD > AC   [Side opposite to greater angle is longer and smaller angle is smaller]