In an acute-angled triangle, express a median in terms of its sides.

Let ΔABC be acute angled triangle where AD is its median with respect side BC.

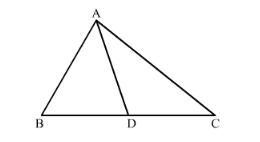
It is known that in any triangle, the sum of the squares of any two sides is equal to twice the square of half of the third side together with twice the square of the median which bisects the third side.

$\therefore A B^{2}+A C^{2}=2 A D^{2}+2\left(\frac{1}{2} B C\right)^{2}$

$A B^{2}+A C^{2}=2 A D^{2}+\frac{1}{2} B C^{2}$

$A D^{2}=\frac{2 A B^{2}+2 A C^{2}-B C^{2}}{4}$

This is the required expression.