Question.
In an equailateral triangle, prove that three times the square of one side is equal to four times the square of one of its altitudes.
In an equailateral triangle, prove that three times the square of one side is equal to four times the square of one of its altitudes.
Solution:
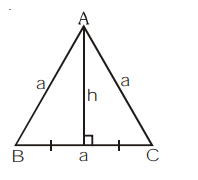
Altitude of equilateral $\Delta=\frac{\sqrt{3}}{2}$ side
$h=\frac{\sqrt{3}}{2} a$
$h^{2}=\frac{3}{4} a^{2}$
$4 h^{2}=3 a^{2}$

Altitude of equilateral $\Delta=\frac{\sqrt{3}}{2}$ side
$h=\frac{\sqrt{3}}{2} a$
$h^{2}=\frac{3}{4} a^{2}$
$4 h^{2}=3 a^{2}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
