In an examination, 56% of the candidates failed in English and 48% failed

Given:

In an examination:

- $56 \%$ of candidates failed in English

$-48 \%$ of candidates failed in science

- $18 \%$ of candidates failed in both English and Science

To Find;

Percentage of students who passed in both subjects.

Let us consider, 

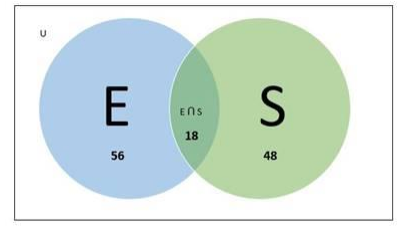
Percentage of candidates who failed in English $=n(E)=56$

Percentage of candidates who failed in Science $=n(S)=48$

Percentage of candidates who failed in English and Science both

$=n(E \cap S)=18$

Percentage of candidates who failed in English only $=n(E-S)$

Percentage of candidates who failed in Science only $=n(S-E)$

Venn diagram:

Now

$n(E-S)=n(E)-n(E \cap S)$

$=56-18$

$=38$

$n(S-E)=n(S)-n(E \cap S)$

$=48-18$

$=30$

Therefore,

Percentage of total candidates who failed =

$n(E-S)+n(S-E)+n(E \cap S)$

$=38+30+18=86 \%$

Now,

The percentage of candidates who passed in both English and

Science $=100-86=14 \%$

Hence

The percentage of candidates who passed in both English and

Science $=14 \%$