In an isosceles triangle ABC, if AB = AC = 13

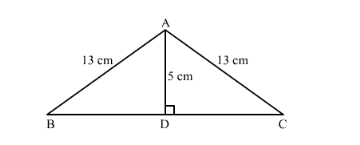
We have given an isosceles triangle and we know that the altitude drawn on the unequal side of the isosceles triangle bisects that side.

Therefore, in $\triangle A D B$ and $\triangle A D C$

$\angle B=\angle C \quad$ (Equal sides have equal angles opposite to them)

$A D=A D$

$\angle A D B=\angle A D C \quad\left(90^{\circ}\right.$ each $)$

$\triangle A D B \cong \triangle A D C \quad$ (AAS congruence theorem)

$\therefore B D=D C$

Now we will use Pythagoras theorem in right angled triangle ADB.

$A B^{2}=A D^{2}+B D^{2}$

Subtracting 25 from both sides we get,

$B D^{2}=169-25$

$B D^{2}=144$

$\therefore B D=12$

Since $B C=2 B D$

$\therefore B C=2 \times 12$

$=24$

Therefore, length of $\mathrm{BC}$ is $24 \mathrm{~cm}$.