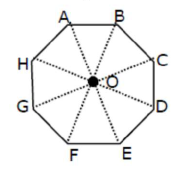
In an octagon $\mathrm{ABCDEFGH}$ of equal side, what is the sum of
$\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{AC}}+\overrightarrow{\mathrm{AD}}+\overrightarrow{\mathrm{AE}}+\overrightarrow{\mathrm{AF}}+\overrightarrow{\mathrm{AG}}+\overrightarrow{\mathrm{AH}}$
If, $\overrightarrow{\mathrm{AO}}=2 \hat{\mathrm{i}}+3 \hat{\mathrm{j}}-4 \hat{\mathrm{k}}$
Correct Option: 1
(1)
$\overrightarrow{A O}+\overrightarrow{O B}=\overrightarrow{A B}$
$\overrightarrow{A O}+\overrightarrow{O C}=\overrightarrow{A C}$
$\overrightarrow{A O}+\overrightarrow{O D}=\overline{A D}$
$\overrightarrow{A O}+\overrightarrow{O E}=\overrightarrow{A E}$
$\overrightarrow{A O}+\overrightarrow{O F}=\overrightarrow{A F}$
$\overrightarrow{A O}+\overrightarrow{O G}=\overrightarrow{A G}$
$\overrightarrow{A O}+\overrightarrow{O H}=\overrightarrow{A H}$
$8 \overrightarrow{\mathrm{AO}}=(\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{AC}}+\overrightarrow{\mathrm{AD}}+\overrightarrow{\mathrm{AE}}+\overrightarrow{\mathrm{AF}}+\overrightarrow{\mathrm{AG}}+\overrightarrow{\mathrm{AH}})$
$=8(2 \hat{\mathrm{i}}+3 \hat{\mathrm{j}}-4 \hat{\mathrm{k}})$
$=16 \hat{\mathrm{i}}+24 \hat{\mathrm{j}}-32 \hat{\mathrm{k}}$