Question.
In any triangle ABC, if the angle bisector of ∠A and perpendicular bisector of BC intersect, prove that they intersect on the circum circle of the triangle ABC.
Solution:
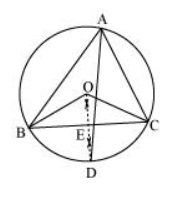
Let perpendicular bisector of side BC and angle bisector of ∠A meet at point D. Let the perpendicular bisector of side BC intersect it at E.
Perpendicular bisector of side BC will pass through circumcentre O of the circle. ∠BOC and ∠BAC are the angles subtended by arc BC at the centre and a point A on the remaining part of the circle respectively. We also know that the angle subtended by an arc at the centre is double the angle subtended by it at any point on the remaining part of the circle.
$\angle B O C=2 \angle B A C=2 \angle A \ldots(1)$
In $\triangle \mathrm{BOE}$ and $\triangle \mathrm{COE}$,
$O E=O E($ Common $)$
$O B=O C$ (Radii of same circle)
$\angle O E B=\angle O E C\left(\right.$ Each $90^{\circ}$ as $\left.O D \perp B C\right)$
$\therefore \triangle B O E \cong \angle C O E(R H S$ congruence rule $)$
$\angle B O E=\angle C O E(B y C P C T) \ldots(2)$
However, $\angle B O E+\angle C O E=\angle B O C$
$\Rightarrow \angle B O E+\angle B O E=2 \angle A$ [Using equations (1) and (2)]
$\Rightarrow 2 \angle B O E=2 \angle A$
$\Rightarrow \angle B O E=\angle A$
$\therefore \angle B O E=\angle C O E=\angle A$
The perpendicular bisector of side BC and angle bisector of ∠A meet at point D.
$\therefore \angle B O D=\angle B O E=\angle A \ldots(3)$
Since $A D$ is the bisector of angle $\angle A$,
$\angle B A D=\frac{\angle A}{2}$
$\Rightarrow 2 \angle B A D=\angle A \ldots(4)$
From equations (3) and (4), we obtain
$\angle B O D=2 \angle B A D$
This can be possible only when point BD will be a chord of the circle. For this, the point D lies on the circum circle.
Therefore, the perpendicular bisector of side BC and the angle bisector of ∠A meet on the circum circle of triangle ABC.

Let perpendicular bisector of side BC and angle bisector of ∠A meet at point D. Let the perpendicular bisector of side BC intersect it at E.
Perpendicular bisector of side BC will pass through circumcentre O of the circle. ∠BOC and ∠BAC are the angles subtended by arc BC at the centre and a point A on the remaining part of the circle respectively. We also know that the angle subtended by an arc at the centre is double the angle subtended by it at any point on the remaining part of the circle.
$\angle B O C=2 \angle B A C=2 \angle A \ldots(1)$
In $\triangle \mathrm{BOE}$ and $\triangle \mathrm{COE}$,
$O E=O E($ Common $)$
$O B=O C$ (Radii of same circle)
$\angle O E B=\angle O E C\left(\right.$ Each $90^{\circ}$ as $\left.O D \perp B C\right)$
$\therefore \triangle B O E \cong \angle C O E(R H S$ congruence rule $)$
$\angle B O E=\angle C O E(B y C P C T) \ldots(2)$
However, $\angle B O E+\angle C O E=\angle B O C$
$\Rightarrow \angle B O E+\angle B O E=2 \angle A$ [Using equations (1) and (2)]
$\Rightarrow 2 \angle B O E=2 \angle A$
$\Rightarrow \angle B O E=\angle A$
$\therefore \angle B O E=\angle C O E=\angle A$
The perpendicular bisector of side BC and angle bisector of ∠A meet at point D.
$\therefore \angle B O D=\angle B O E=\angle A \ldots(3)$
Since $A D$ is the bisector of angle $\angle A$,
$\angle B A D=\frac{\angle A}{2}$
$\Rightarrow 2 \angle B A D=\angle A \ldots(4)$
From equations (3) and (4), we obtain
$\angle B O D=2 \angle B A D$
This can be possible only when point BD will be a chord of the circle. For this, the point D lies on the circum circle.
Therefore, the perpendicular bisector of side BC and the angle bisector of ∠A meet on the circum circle of triangle ABC.
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
