In below fig, ray OS stand on a line POQ.

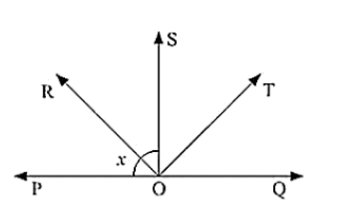
Solution:

Given,

Ray OS stand on a line POQ

Ray OR and Ray OT are angle bisectors of ∠POS and ∠SOQ respectively

∠POS = x

∠POS and ∠SOQ is linear pair

∠POS + ∠QOS = 180°

x + QOS = 180

QOS = 180 - x

Now, ray or bisector POS

∠ROS = 1/2 ∠POS

x/2

ROS = x/2    [Since POS = x]

Similarly ray OT bisector QOS

∠TOS = 1/2 ∠QOS

= (180 - x)/2    [QOS = 180 - x]

= 90 - x/2

Hence, ∠ROT = ∠ROS + ∠ROT

= x/2 + 90 - x/2

= 90

∠ROT = 180°