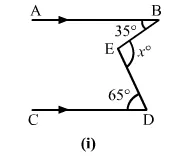
In each of the figures given below, AB || CD. Find the value of x in each case.

(i)

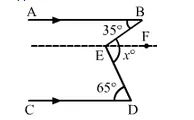
Draw $E F\|A B\| C D$.

Now, $A B \| E F$ and $B E$ is the transversal.

Then,

$\angle A B E=\angle B E F \quad[$ Alternate Interior Angles $]$

$\Rightarrow \angle B E F=35^{\circ}$

Again. $E F \| C D$ and $\mathrm{DE}$ is the transversal.

Then,

$\angle D E F=\angle F E D$

$\Rightarrow \angle F E D=65^{\circ}$

$\therefore x^{\circ}=\angle B E F+\angle F E D$

$=(35+65)^{\circ}$

$=100^{\circ}$

or, $x=100$

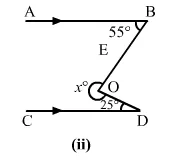
(ii)

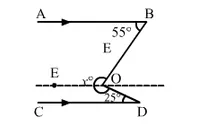
Draw $E O\|A B\| C D$.

Then, $\angle E O B+\angle E O D=x^{\circ}$

Now, $E O \| A B$ and $B O$ is the transversal.

$\therefore \angle E O B+\angle A B O=180^{\circ} \quad[$ Consecutive Interior Angles $]$

$\Rightarrow \angle E O B+55^{\circ}=180^{\circ}$

$\Rightarrow \angle E O B=125^{\circ}$

Again, $E O \| C D$ and $D O$ is the transversal.

$\therefore \angle E O D+\angle C D O=180^{\circ} \quad$ [Consecutive Interior Angles]

$\Rightarrow \angle E O D+25^{\circ}=180^{\circ}$

$\Rightarrow \angle E O D=155^{\circ}$

Therefore,

$x^{\circ}=\angle E O B+\angle E O D$

$=(125+155)^{\circ}$

$=280^{\circ}$

or, $x=280$

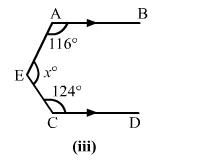
(iii)

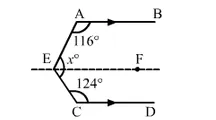
Draw $E F\|A B\| C D$.

Then, $\angle A E F+\angle C E F=x^{\circ}$

Now, $E F \| A B$ and $A E$ is the transversal.

$\therefore \angle A E F+\angle B A E=180^{\circ} \quad$ [Consecutive Interior Angles]

$\Rightarrow \angle A E F+116=180$

$\Rightarrow \angle A E F=64^{\circ}$

Again, $E F \| C D$ and $C E$ is the transversal.

$\angle C E F+\angle E C D=180^{\circ} \quad[$ Consecutive Interior Angles $]$

$\Rightarrow \angle C E F+124=180$

$\Rightarrow \angle C E F=56^{\circ}$

Therefore,

$x^{\circ}=\angle A E F+\angle C E F$

$=(64+56)^{\circ}$

$=120^{\circ}$

or, $x=120$