In each of the figures given below, ABCD is a rhombus. Find the value of x and y in each case.

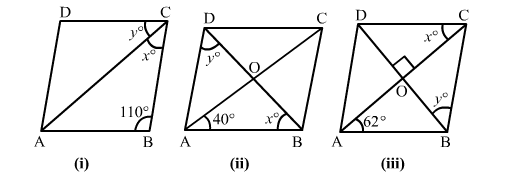
ABCD is a rhombus and a rhombus is also a parallelogram. A rhombus has four equal sides.

(i) $\ln \triangle A B C, \angle B A C=\angle B C A=\frac{1}{2}(180-110)=35^{\circ}$

i.e., x = 35o   
Now, ∠​B + ∠C = 180o                 (Adjacent angles are supplementary)  ​
But ∠​C​ = x + y = 70o 
 ⇒​ y = 70o  −  x  
 ⇒​y =  70o − 35o = 35o
 Hence, x = 35o; y = 35o

(ii) The diagonals of a rhombus are perpendicular bisectors of each other.
   So, in ∆​AOB, ​∠OAB = 40o, ∠AOB = 90o and ∠ABO = 180o − (40o + 90o) = 50o
   ∴ ​x = 50o
   In ∆​AB​D, AB = AD
   So, ∠ABD = ​∠ADB = ​50o
   Hence, x = 50o;  y = 50o

​(iii) ∠​BAC = ∠​DCA                   (Alternate interior angles)​
     i.e., x  = 62o  
     In ∆BOC, ∠​BCO =  62o              [In ∆​ ABC, AB = BC, so ∠​BAC = ∠​ACB]
    Also, ∠​BOC = 90o
  ∴ ∠​OBC = 180o − (90o + 62o) = 28o
  Hence, x = 62o; y = 28o