In each of the figures given below, an altitude is drawn to the hypotenuse by a right-angled triangle.

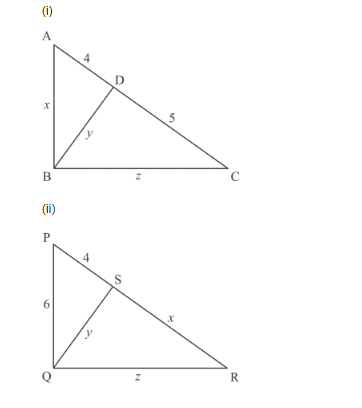
(i) $\triangle A B C$ is right angled triangle right angled at $B$

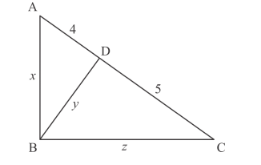
$A B^{2}+B C^{2}=A C^{2}$

$x^{2}+z^{2}=(4+5)^{2}$

$x^{2}+z^{2}=9^{2}$

$x^{2}+z^{2}=81$......$(i)$

$\triangle B D A$ is right triangle right angled at $\mathrm{D}$

$B D^{2}+A D^{2}=A B^{2}$

$y^{2}+4^{2}=x^{2}$

$y^{2}+16=x^{2}$

$16=x^{2}-y^{2}$...(ii)

$\triangle B D C$ is right triangle right angled at $D$

$B D^{2}+D C^{2}=B C^{2}$

$y^{2}+25=z^{2}$

$25=z^{2}-y^{2}$$\ldots \ldots($ iii $)$

By canceling equation(i) and(ii) by elimination method, we get

y canceling and by elimination method we get

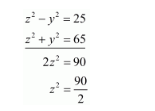
$z^{2}=45$

$z=\sqrt{45}$

$z=\sqrt{3 \times 3 \times 5}$

$z=3 \sqrt{5}$

Now, substituting $z^{2}=45$ in equation (iv) we get

$y^{2}+z^{2}=65$

$y^{2}+45=65$

$y^{2}=65-45$

$y^{2}=20$

$y=\sqrt{20}$

$y=\sqrt{2 \times 2 \times 5}$

$y=2 \sqrt{5}$

Now, substituting $y^{2}=20$ in equation (ii) we get

$x^{2}-y^{2}=16$

$x^{2}-20=16$

$x^{2}=16+20$

$x^{2}=36$

$x=\sqrt{36}$

$x=\sqrt{6 \times 6}$

$x=6$

Hence the values of $x, y, z$ is $6,2 \sqrt{5}, 3 \sqrt{5}$

(ii) $\triangle P Q R$ is a right triangle, right angled at $Q$

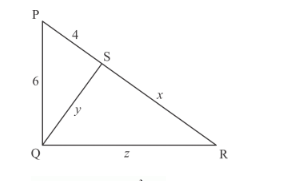
$6+z^{2}=(4+x)^{2}$

$36+z^{2}=16+x^{2}+8 x$

$z^{2}-x^{2}-8 x=16-36$

$z^{2}-x^{2}-8 x=-20 \ldots \ldots$ (i)

$\Delta Q S P$ is a right triangle right angled at $S$

$Q S^{2}+P S^{2}=P Q^{2}$

$y^{2}+4^{2}=6^{2}$

$y^{2}+16=36$

$y^{2}=36-16$

$y^{2}=20$

$y=\sqrt{20}$

$y=\sqrt{2 \times 2 \times 5}$

$y=2 \sqrt{5}$

$\triangle Q S R$ is a right triangle right angled at $S$

$Q S^{2}+R S^{2}=Q R^{2}$

$y^{2}+x^{2}=z^{2}$.....(2)

Now substituting $y^{2}+x^{2}=z^{2}$ in equation (i) we get

$y^{2}+x^{2}-x^{2}-8 x=-20$

$y^{2}+x^{2}-x^{2}-8 x=-20$

$y^{2}-8 x=-20$$\ldots \ldots(i i i)$

Now substituting $y^{2}=20$ in equation (iii) we get

$y^{2}-8 x=-20$

$20-8 x=-20$

$-8 x=-20-20$

$-8 x=-40$

$x=\frac{40}{8}$

$x=5$

Now substituting $x=5$ and $y^{2}=20$ in equation (ii) we get

$y^{2}+x^{2}=z^{2}$

$20+5^{2}=z^{2}$

$20+25=z^{2}$

$45=z^{2}$

$\sqrt{3 \times 3 \times 5}=z^{2}$

$3 \sqrt{5}=z$

Hence the value of $x, y$ and $z$ are $5,2 \sqrt{5}, 3 \sqrt{5}$