In each of the following figures, you find who triangles

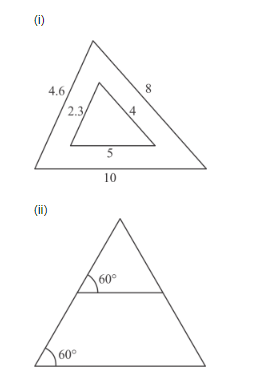
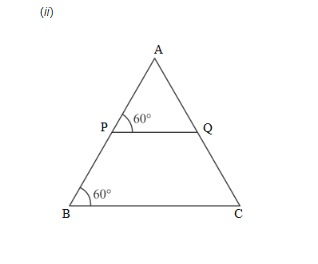
(i) In two triangles, we observe that

In similar triangle corresponding sides are proportional to each other.

Therefore, by SSS-criterion of similarity,

yes two triangles are similar

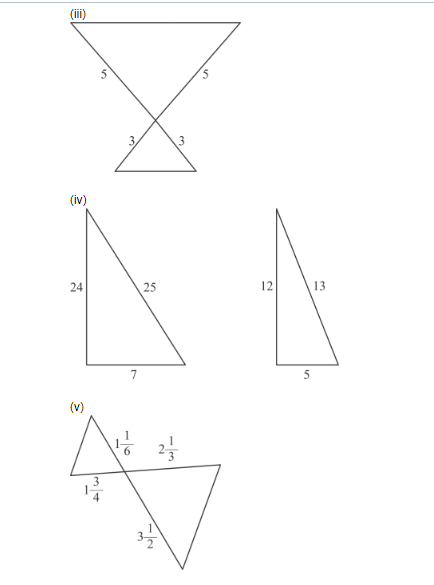
PQ || BC             (Corresponding angles formed are equal)

In ΔAPQ and ΔABC,

$\angle A P Q=\angle B$ (Corresponding angles)

      $\angle P A Q=\angle B A C$ (Common)

So, $\triangle \mathrm{APQ}-\Delta \mathrm{ABC}$ (A.A Similarity)

yes two triangles are similar

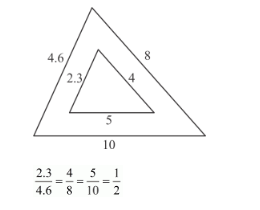
(iii) In two triangle, we observe that

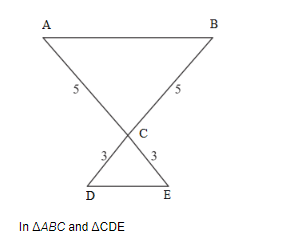
$\frac{C D}{C E}=\frac{C B}{C A}$

$\angle A C B=\angle D C E$ (Vertically opposite angles)

$\triangle A B C-\triangle C D E$ (SAS Similarity)

yes two triangles are similar

(iv) In two triangle, we observe that

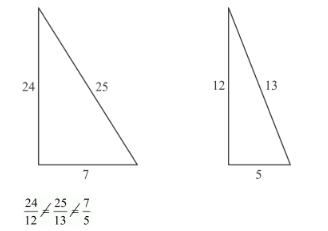
In two triangles corresponding sides are not proportional to each other.

No two triangles are not similar.

(v) In two triangle, we observe that

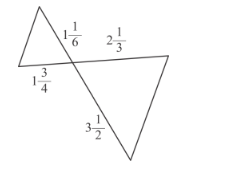
In two triangles corresponding sides are not proportional to each other.

No two triangles are not similar.