In Fig. (10).22, the sides BA and CA have been produced such that: BA = AD and CA = AE. Prove that segment DE ∥ BC.

Question:
In Fig. (10).22, the sides BA and CA have been produced such that: BA = AD and CA = AE. Prove that segment DE ∥ BC.

Solution:

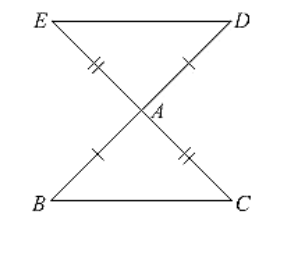
Given that, the sides BA and CA have been produced such that BA = AD and CA = AE and given to prove DE ∥ BC Consider triangle BAC and DAE,

We have

BA = AD and CA= AE [given in the data]

And also ∠BAC = ∠DAE [vertically opposite angles]

So, by SAS congruence criterion, we have

∠BAC ≃ ∠DAE

BC = DE and ∠DEA = ∠BCA, ∠EDA = ∠CBA

[Corresponding parts of congruent triangles are equal]

Now, DE and BC are two lines intersected by a transversal DB such that ∠DEA = ∠BCA i.e.. alternate angles are equal Therefore, DE, BC ∥ BC.