Question:
In Fig., prove that:
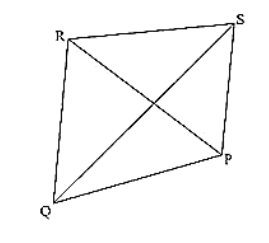
(i) CD + DA + AB + BC > 2AC
(ii) CD + DA + AB > BC
Solution:
To prove
(i) CD + DA + AB + BC > 2AC
(ii) CD + DA+ AB > BC
From the given figure,
We know that, in a triangle sum of any two sides is greater than the third side
(i) So,
In ΔABC, we have
AB + BC > AC .... (i)
In ΔADC, we have
CD + DA > AC .... (ii)
Adding (i) and (ii), we get
AB + BC + CD + DA > AC + AC
AB + BC + CD + DA > 2AC
(ii) Now, In Δ ABC, we have,
AB + AC > BC ... (iii)
And in ΔADC, we have
CD + DA > AC
Add AB on both sides
CD + DA + AB > AC + AB
From equation (iii) and (iv), we get,
CD + DA + AB > AC + AB > BC
CD + DA + AB > BC
Hence proved