Question:
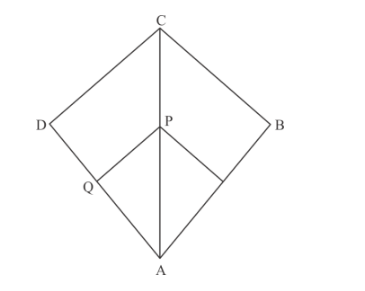
In Figure $3, P Q \| C D$ and $P R \| C B$. Prove that $\frac{A Q}{Q D}=\frac{A R}{R B}$.
Solution:
Given that:
$P Q \| C D$ and $P R \| C B$, then we to prove that $\frac{A Q}{Q D}=\frac{A R}{R B}$
The following diagram is given
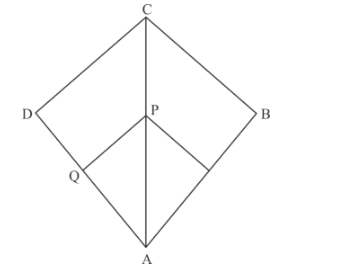
We can easily see that, in the above figure 
are similar triangles, and also the 
are similar triangles.
Now, we have the following properties of similar triangles,
$\frac{A Q}{Q D}=\frac{A P}{P C}$ ................(1)
$\frac{A R}{R B}=\frac{A P}{P C}$ ................(2)
From equation (1) and Equation (2), we get
$\frac{A Q}{Q D}=\frac{A R}{R B}$
Hence proved.