In Figure 6, P and Q are the midpoints of the sides CA and CB

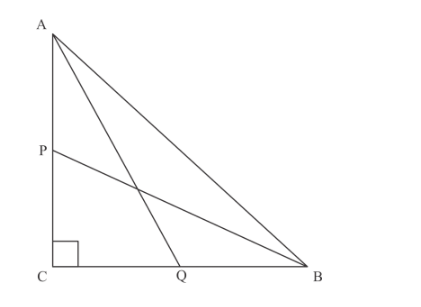
In the given figure P and Q are the mid points of AC and BC, the we have to prove that 

The following figure is given.

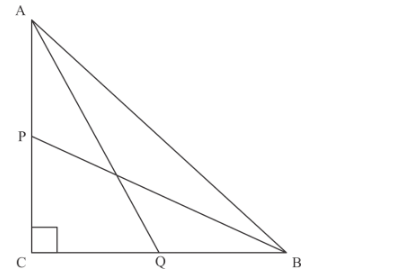
Using Pythagoras theorem in $\triangle A B C$, we get

AB2 = AC2 + BC2…… (1)

Similarly, by using Pythagoras theorem in $\triangle A C Q$ and $\triangle B C P$, we get

AQ2 = CQ2 + AC2…… (2)

BP2 = CP2 + BC2…… (3)

Now adding equation (2) and equation (3), we get

$A Q^{2}+B P^{2}=C Q^{2}+C P^{2}+A C^{2}+B C^{2}$

$A Q^{2}+B P^{2}=\left(\frac{B C}{2}\right)^{2}+\left(\frac{A C}{2}\right)^{2}+A B^{2}$ from equation (1)

$A Q^{2}+B P^{2}=\frac{A C^{2}+B C^{2}}{4}+A B^{2}$

$A Q^{2}+B P^{2}=\frac{A B^{2}}{4}+A B^{2}$

$A Q^{2}+B P^{2}=\frac{5 A B^{2}}{4}$..........(4)

Now multiply equation (4) by 4, we get

$4 \times\left(A Q^{2}+B P^{2}\right)=4 \times \frac{5 A B^{2}}{4}$

$4\left(A Q^{2}+B P^{2}\right)=5 A B^{2}$

Hence proved.