Question:
In figure 9.37, AM ⊥ BC and AN is the bisector of ∠A. If ∠B = 65° and ∠C = 33°, find ∠MAN.
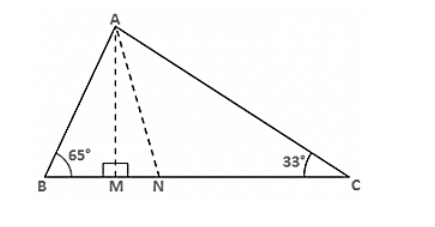
Solution:
Let ∠BAN = ∠NAC = x [∵ AN bisects ∠A]
∴ ∠ANM = x + 33° [Exterior angle property]
In ΔAMB
∠BAM = 90° − 65° = 25° [Exterior angle property]
∴ ∠MAN = ∠BAN − ∠BAM = (x − 25)°
Now in ΔMAN,
(x - 25)° + (x + 33)° + 90° = 180° [Angle sum property]
⇒ 2x + 8° = 90°
⇒ 2x = 82°
⇒ x = 41°
∴ MAN = x − 25°
= 41° − 25°
= 16°