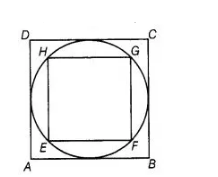
In figure, a square is inscribed in a circle

False

Given diameter of circle is $d$.

$\therefore$ Diagonal of inner square $=$ Diameter of circle $=\mathrm{d}$

Let side of inner square EFGH be $\mathrm{x}$.

$\therefore$ In right angled $\triangle \mathrm{EFG}$,

$E G^{2}=E F^{2}+F G^{2}$ [by Pythagoras theorem]

$\Rightarrow \quad d^{2}=x^{2}+x^{2}$

$\Rightarrow \quad d^{2}=2 x^{2} \Rightarrow x^{2}=\frac{d^{2}}{2}$

$\therefore \quad$ Area of inner square $E F G H=(\text { Side })^{2}=x^{2}=\frac{d^{2}}{2}$

But side of the outer square ABCS = Diameter of circle = d

∴                                                 Area of outer square = d2

Hence, area of outer square is not equal to four times the area of the inner square.