In figure, a square of diagonal 8 cm

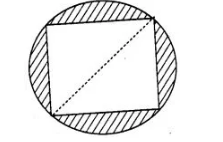
Let the side of a square be a and the radius of circle be r.

Given that, length of diagonal of square = 8 cm

$\Rightarrow \quad a \sqrt{2}=8$

$\Rightarrow \quad a=4 \sqrt{2} \mathrm{~cm}$

Now,

Diagonal of a square = Diameter of a circle

$\Rightarrow \quad$ Diameter of circle $=8$

$\Rightarrow$ Radius of circle $=r=\frac{\text { Diameter }}{2}$

$\Rightarrow$ $r=\frac{8}{2}=4 \mathrm{~cm}$

$\therefore$ Area of circle $=\pi r^{2}=\pi(4)^{2}$

$=16 \pi \times \mathrm{cm}^{2}$

and

Area of square $=a^{2}=(4 \sqrt{2})^{2}$

$=32 \mathrm{~cm}^{2}$

So, the area of the shaded region = Area of circle – Area of square

= (16π – 32) cm2

Hence, the required area of the shaded region is (16π – 32) cm2.