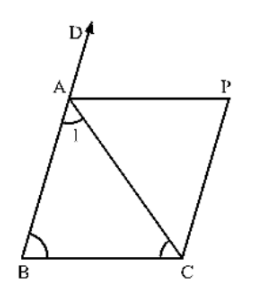
In figure, AB = AC and CP ∥ BA and AP is the bisector of exterior ∠CAD of ∆ABC.

Solution:

Given,

AB = AC and CD ∥ BA and AP is the bisector of exterior ∠CAD of ΔABC

To prove:

(i) ∠PAC = ∠BCA

(ii) ABCP is a parallelogram.

Proof:

(i) We have,

AB = AC

⟹ ∠ACB = ∠ABC      [Opposite angles of equal sides of triangle are equal]

Now, ∠CAD = ∠ABC + ∠ACB

⟹ ∠PAC + ∠PAD = 2∠ACB          [∴ ∠PAC = ∠PAD]

⟹ 2∠PAC = 2∠ACB

⟹ ∠PAC = ∠ACB

(ii) Now,

∠PAC = ∠BCA

⟹ AP ∥ BC and CP ∥ BA     [Given]

Therefore, ABCP is a parallelogram.