Question:
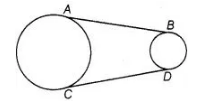
In figure, AB and CD are common tangents to two circles of unequal radii. Prove that AB = CD
Solution:
Given AS and CD are common tangent to two circles of unequal radius
To prove AB = CD
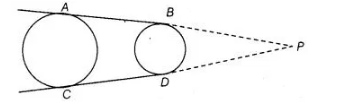
Construction Produce $A B$ and $C D$, to intersect at $P$.
Proof $P A=P C$
[the length of tangents drawn from an internal point to a circle are equal]
Also, $P B=P D$
[the lengths of tangents drawn from an internal point to a circle are equal]
$\therefore$ $P A-P B=P C-P D$
$A B=C D$
Hence proved.
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
