Question:
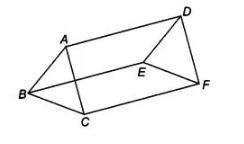
In figure, $A B\|D E, A B=D E, A C\| D F$ and $A C=O F$. Prove that $B C \| E F$ and $B C=E F$.
Solution:
Given In figure AB || DE and AC || DF, also AB = DE and AC = DF
To prove BC ||EF and BC = EF
Proof In quadrilateral ABED, AB||DE and AB = DE
So, ABED is a parallelogram. AD || BE and AD = BE
Now, in quadrilateral ACFD, AC || FD and AC = FD …..(i)
Thus, ACFD is a parallelogram.
AD || CF and AD = CF …(ii)
From Eqs. (i) and (ii), AD = BE = CF and CF || BE …(iii)
Now, in quadrilateral BCFE, BE = CF
and BE||CF [from Eq. (iii)]
So, BCFE is a parallelogram. BC = EF and BC|| EF . Hence proved.
Comments
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
