In figure, AB is a diameter of the circle,

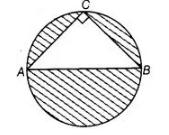
Given,                                          AC = 6 cm and BC = 8 cm

We know that, triangle in a semi-circle with hypotenuse as diameter is right angled triangle.

$\therefore \quad \angle C=90^{\circ}$

In right angled $\triangle A C B$, use Pythagoras theorem,

$\therefore$ $A B^{2}=A C^{2}+C B^{2}$

$\Rightarrow \quad A B^{2}=100$

$\Rightarrow \quad A B=10 \mathrm{~cm} \quad$ [since, side cannot be negative]

$\therefore$ Area of $\triangle A B C=\frac{1}{2} \times B C \times A C=\frac{1}{2} \times 8 \times 6=24 \mathrm{~cm}^{2}$

Here, diameter of circle, $A B=10 \mathrm{~cm}$

$\therefore \quad$ Radius of circle, $r=\frac{10}{2}=5 \mathrm{~cm}$

Area of circle $=\pi r^{2}=3.14 \times(5)^{2}$

$=3.14 \times 25=78.5 \mathrm{~cm}^{2}$

Area of the shaded region $=$ Area of circle $-$ Area of $\triangle A B C$

$=78.5-24=54.5 \mathrm{~cm}^{2}$