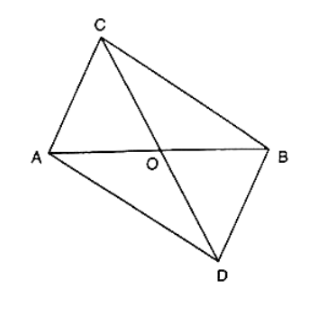
Question:
In figure, ABC and ABD are two triangles on the base AB. If line segment CD is bisected by AB at O, show that ar(ΔABC) = ar(ΔABD).
Solution:
Given that CD is bisected by AB at O
To prove: ar(ΔABC) = ar(ΔABD).
Construction: Draw CP ⊥ AB and DQ ⊥ AB.
Proof:
ar(ΔABC) = 1/2 × AB × CP⋅⋅⋅⋅⋅ (1)
ar(ΔABD) = 1/2 × AB × DQ ⋅⋅⋅⋅ (2)
In ΔCPO and ΔDQO
∠CPO = ∠DQO [Each 90°]
Given that, CO = OD
∠COP = ∠DOQ [Vertically opposite angles are equal]
Then, ΔCPO ≅ ΔDQO [By AAS condition]
∴ CP = DQ (3) [C.P.C.T]
Compare equation (1), (2) and (3)
∴ ar(ΔABC) = ar(ΔABD).