In figure ABC and BDE are two equilateral triangles such that D is the midpoint of BC.

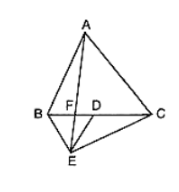
Given that ABC and BDE are two equilateral triangles.

Let AB = BC = CA = x. Then, BD = x/2 = DE = BE

(i) We have,

$\operatorname{ar}(\Delta \mathrm{ABC})=\frac{\sqrt{3}}{4} \mathrm{x}^{2}$ and $\operatorname{ar}(\Delta \mathrm{BDE})=\frac{\sqrt{3}}{4}\left(\frac{\mathrm{X}}{2}\right)^{2}=\frac{1}{4} \times \frac{\sqrt{3}}{4} \mathrm{x}^{2}$

Therefore, ar(ΔBDE) = 1/4 ar(ΔABC).

(ii) It is given that triangles, ABC and BED are equilateral triangles

∠ ACB = ∠DBE = 60°

⇒ BE ∥ AC (Since, Alternative angles are equal)

Trinagles BAF and BEC are on the same base BE and between same parallels BF and AC.

Therefore, ar(ΔBAE) = ar(ΔBEC)

⇒ ar(ΔBAE) = 2ar(ΔBDE)      [Since , ED is a median of triangle EBC; ar(ΔBEC) = 2ar(ΔBDE) ]

∴ ar(ΔBDE) = (1/2) ar(ΔBAE)

(iii) Since, triangles ABC and BDE are equilateral triangles

∴ ∠ABC = 60° and ∠BDE = 60°

∠ABC = ∠BDE

⇒ AB ∥ DE     (since, alternate angles are equal)

Triangles BED and AED are on the same base ED and between same parallels AB and DE.

Therefore, ar(ΔBED) = ar(ΔAED)

⇒ ar(ΔBED) − ar(ΔEFD) = ar(ΔAED) − ar(ΔEFD)

⇒ ar(ΔBEF) = ar(ΔAFD)

(iv) Since ED is the median of triangle BEC

Therefore, ar(ΔBEC) = 2ar(ΔBDE)

⇒ ar(ΔBEC) = 2 × (1/2) ar(ΔABC)    [From 1, ar(ΔBDE) = (1/2) ar(ΔABC)]

⇒ ar(ΔBEC) = (1/2) ar(ΔABC)

⇒ ar(ΔABC) = 2ar(ΔBEC)

(v) ar(ΔAFC) = ar(ΔAFD) + ar(ΔADC)

⇒ ar(ΔBFE) + (1/2) ar(ΔABC)           [using part (iii) , and AD is the median of triangle ABC ]

= ar(ΔBFE) + (1/2) × 4ar(ΔBDE)             (using part (i))

= ar(ΔBFE) = 2ar(ΔFED)  ⋅⋅⋅ (3)

ar(ΔBDE) = ar(ΔBFE) + ar(ΔFED)

⇒ 2ar(ΔFED) + ar(ΔFED)

⇒ 3ar(ΔFED) ⋅⋅⋅⋅ (4)

From 2, 3 and 4 we get,

ar(ΔAFC) = 2ar(ΔFED) + 2 × 3 ar(ΔFED) = 8 ar(ΔFED)

ar(ΔFED) = (1/8) ar(ΔAFC)

(vi) Let h be the height of vertex E, corresponding to the side BD in triangle BDE.

Let H be the height of vertex A, corresponding to the side BC in triangle ABC

From part (i)

ar(ΔBDE) = (1/4) ar(ΔABC)

⇒ (1/2) × BD × h = (1/4) (1/2 × BC × h)

⇒ BD × h = (1/4)(2BD × H)

⇒ h = (1/2) H    ⋅⋅⋅ (1)

From part (iii)

ar(ΔBFE) = ar(ΔAFD)

ar(ΔBFE) = (1/2) × FD × H

ar(ΔBFE) = (1/2) × FD × 2h

ar(ΔBFE) = 2((1/2) × FD × h)

ar(ΔBFE) = 2ar(ΔEFD)