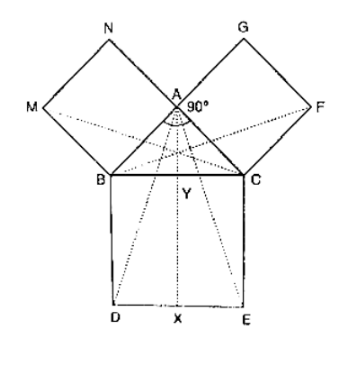
In figure, ABC is a right angled triangle at A, BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively.

(i) In ΔMBC and ΔABD, we have

MB = AB

BC = BD

And ∠MBC = ∠ABD        [since, ∠MBC and ∠ABC are obtained by adding ∠ABC to a right angle.]

So, by SAS congruence criterion, we have

ΔMBC ≅ ΔABD

⇒ ar(ΔMBC) = ar(ΔABD)    ⋅⋅⋅⋅⋅ (1)

(ii) Clearly, triangle ABC and rectangle BYXD are on the same base BD and between the same parallels AX and BD.

∴ ar(ΔABD) = (1/2) ar(rect BYXD)

⇒ ar (rect BYXD) = 2ar(ΔABD)

⇒ ar (rect BYXD) = 2ar(ΔMBC)  ⋅⋅⋅⋅ (2)           [From  equ .1]

(iii) Since triangles MBC and square MBAN are on the same base Mb and between the same parallels MB and NC.

∴ 2ar(ΔMBC) = ar(MBAN)  ⋅⋅⋅⋅⋅ (3)

From equ. 2 and 3, we have

ar(sq. MBAN) = ar(rect BYXD)

(iv) In triangles FCB and ACE, we have

FC = AC

CB = CE

And, ∠FCB = ∠ACE    [since, ∠FCB and ∠ACE are obtained by adding ∠ACB to a right angle.]

So, by SAS congruence criterion, we have

ΔFCB ≅ ΔACE

(v) We have,

ΔFCB ≅ ΔACE

⇒ ar(ΔFCB) = ar(ΔACE)

Clearly, triangle ACE and rectangle CYXE are on the same base CE and between same parallels CE and AX.

∴ 2ar(ΔACE) = ar(CYXE)

⇒ 2ar(ΔFCB) = ar(ΔCYXE) ⋅⋅⋅ (4)

(vi) Clearly, triangle FCb and rectangle FCAG are on the same base FC and between the same parallels FC and BG.

∴ 2ar(ΔFCB) = ar(FCAG)  ⋅⋅⋅⋅ (5)

From 4 and 5, we get

ar(CYXE) = ar(ACFG)

(vii) Applying Pythagoras theorem in triangle ACB, we have

$B C^{2}=A B^{2}+A C^{2}$

⇒ BC × BD = AB × MB + AC × FC

⇒ ar(BCED) = ar(ABMN) + ar(ACFG)