In figure, ABCD and AEFD are two parallelograms. Prove that
(i) PE = FQ
(ii) ar(ΔAPE) : ar(ΔPFA) = ar(ΔQFD): ar(ΔPFD)
(iii) ar(ΔPEA) = ar(ΔQFD)
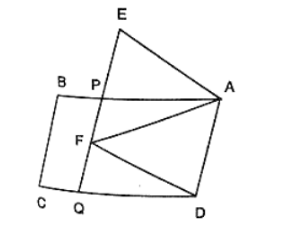
Given that, ABCD and AEFD are two parallelograms
(i) In triangles, EPA and FQD
∠PEA = ∠QFD [corresponding angles]
∠EPA=∠FQD [corresponding angles]
PA = QD [opposite sides of parallelogram]
Then, ΔEPA ≅ ΔFQD [By AAS condition]
Therefore, EP = FQ [C.P.C.T]
(ii) Since triangles, PEA and QFD stand on equal bases PE and FQ lies between the same parallels EQ and AD
Therefore, ar(ΔPEA) = ar(ΔQFD) ... (1)
Since, triangles PEA and PFD stand on the same base PF and between same parallels PF and AD
Therefore, ar(ΔPFA) = ar(ΔPFD) .... (2)
Divide the equation 1 by equation 2
ar(ΔPEA) ar(ΔPFA) = ar(ΔQFD) ar(ΔPFD)
(iii) From part (i),
ΔEPA ≅ ΔFQD
Then, ar(ΔPEA) = ar(ΔQFD).