Question.
In figure, $A B D$ is a right triangle right angled at $A$ and $A C \perp B D$. Show that
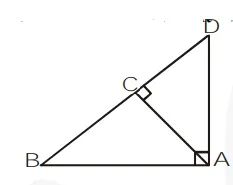
(i) $\mathrm{AB}^{2}=\mathrm{BC} \cdot \mathrm{BD}$
(ii) $\mathrm{AC}^{2}=\mathrm{BC} . \mathrm{DC}$
(iii) $\mathrm{AD}^{2}=\mathrm{BD} \cdot \mathrm{CD}$
In figure, $A B D$ is a right triangle right angled at $A$ and $A C \perp B D$. Show that
(i) $\mathrm{AB}^{2}=\mathrm{BC} \cdot \mathrm{BD}$
(ii) $\mathrm{AC}^{2}=\mathrm{BC} . \mathrm{DC}$
(iii) $\mathrm{AD}^{2}=\mathrm{BD} \cdot \mathrm{CD}$
Solution:
In the given figure, we have
$\Delta \mathrm{ABC} \sim \Delta \mathrm{DAC} \sim \Delta \mathrm{DBA}$
(i) $\triangle \mathrm{ABC} \sim \Delta \mathrm{DBA}$
$\Rightarrow \frac{\operatorname{ar}(\Delta A B C)}{\operatorname{ar}(\Delta D B A)}=\frac{A B^{2}}{D B^{2}} \Rightarrow \frac{\frac{1}{2}(B C) \times(A C)}{\frac{1}{2}(B D) \times(A C)}=\frac{A B^{2}}{D B^{2}} \Rightarrow \quad A B^{2}=B C \cdot B D$
(ii) $\triangle \mathrm{ABC} \sim \Delta \mathrm{DAC}$
$\Rightarrow \frac{\operatorname{ar}(\Delta A B C)}{\operatorname{ar}(\triangle D A C)}=\frac{A C^{2}}{D C^{2}} \Rightarrow \frac{\frac{1}{2}(B C) \times(A C)}{\frac{1}{2}(D C) \times(A C)}=\frac{A C^{2}}{D C^{2}} \Rightarrow \quad A C^{2}=B C . D C$
(iii) $\Delta \mathrm{DAC} \sim \Delta \mathrm{DBA}$
$\Rightarrow \frac{\operatorname{ar}(\triangle \mathrm{DAC})}{\operatorname{ar}(\triangle \mathrm{DBA})}=\frac{\mathrm{DA}^{2}}{\mathrm{DB}^{2}} \Rightarrow \frac{\frac{1}{2}(\mathrm{CD}) \times(\mathrm{AC})}{\frac{1}{2}(\mathrm{BD}) \times(\mathrm{AC})}=\frac{\mathrm{AD}^{2}}{\mathrm{BD}^{2}} \Rightarrow \quad \mathrm{AD}^{2}=\mathrm{BD} \cdot \mathrm{CD}$
In the given figure, we have
$\Delta \mathrm{ABC} \sim \Delta \mathrm{DAC} \sim \Delta \mathrm{DBA}$
(i) $\triangle \mathrm{ABC} \sim \Delta \mathrm{DBA}$
$\Rightarrow \frac{\operatorname{ar}(\Delta A B C)}{\operatorname{ar}(\Delta D B A)}=\frac{A B^{2}}{D B^{2}} \Rightarrow \frac{\frac{1}{2}(B C) \times(A C)}{\frac{1}{2}(B D) \times(A C)}=\frac{A B^{2}}{D B^{2}} \Rightarrow \quad A B^{2}=B C \cdot B D$
(ii) $\triangle \mathrm{ABC} \sim \Delta \mathrm{DAC}$
$\Rightarrow \frac{\operatorname{ar}(\Delta A B C)}{\operatorname{ar}(\triangle D A C)}=\frac{A C^{2}}{D C^{2}} \Rightarrow \frac{\frac{1}{2}(B C) \times(A C)}{\frac{1}{2}(D C) \times(A C)}=\frac{A C^{2}}{D C^{2}} \Rightarrow \quad A C^{2}=B C . D C$
(iii) $\Delta \mathrm{DAC} \sim \Delta \mathrm{DBA}$
$\Rightarrow \frac{\operatorname{ar}(\triangle \mathrm{DAC})}{\operatorname{ar}(\triangle \mathrm{DBA})}=\frac{\mathrm{DA}^{2}}{\mathrm{DB}^{2}} \Rightarrow \frac{\frac{1}{2}(\mathrm{CD}) \times(\mathrm{AC})}{\frac{1}{2}(\mathrm{BD}) \times(\mathrm{AC})}=\frac{\mathrm{AD}^{2}}{\mathrm{BD}^{2}} \Rightarrow \quad \mathrm{AD}^{2}=\mathrm{BD} \cdot \mathrm{CD}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.