In figure, altitudes $\mathrm{AD}$ and $\mathrm{CE}$ of $\triangle \mathrm{ABC}$ intersect each other at the point $\mathrm{P}$.
Question.
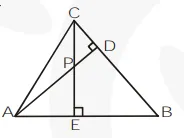
In figure, altitudes $\mathrm{AD}$ and $\mathrm{CE}$ of $\triangle \mathrm{ABC}$ intersect each other at the point $\mathrm{P}$. Show that :
(i) $\triangle \mathrm{AEP} \sim \Delta \mathrm{CDP}$
(ii) $\triangle \mathrm{ABD} \sim \Delta \mathrm{CBE}$
(iii) $\triangle \mathrm{AEP} \sim \triangle \mathrm{ADB}$
(iv) $\Delta \mathrm{PDC} \sim \Delta \mathrm{BEC}$
In figure, altitudes $\mathrm{AD}$ and $\mathrm{CE}$ of $\triangle \mathrm{ABC}$ intersect each other at the point $\mathrm{P}$. Show that :

(i) $\triangle \mathrm{AEP} \sim \Delta \mathrm{CDP}$
(ii) $\triangle \mathrm{ABD} \sim \Delta \mathrm{CBE}$
(iii) $\triangle \mathrm{AEP} \sim \triangle \mathrm{ADB}$
(iv) $\Delta \mathrm{PDC} \sim \Delta \mathrm{BEC}$
Solution:
(i) In $\triangle \mathrm{AEP}$ and $\triangle \mathrm{CDP}$,
$\angle \mathrm{APE}=\angle \mathrm{CPD}$ (vertically opposite angles)
$\angle \mathrm{AEP}=\angle \mathrm{CDP}=90^{\circ}$
$\therefore \quad$ By AA similarity
$\Delta \mathrm{AEP} \sim \Delta \mathrm{CDP}$
(ii) In $\triangle \mathrm{ABD}$ and $\triangle \mathrm{CBE}$,
$\angle \mathrm{ABD}=\angle \mathrm{CBE}($ common $)$
$\angle \mathrm{ADB}=\angle \mathrm{CEB}=90^{\circ}$
$\therefore$ By AA similarity
$\Delta \mathrm{ABD} \sim \Delta \mathrm{CBE}$
(iii) In $\triangle \mathrm{AEP}$ and $\triangle \mathrm{ADB}$,
$\angle \mathrm{PAE}=\angle \mathrm{DAB}($ common $)$
$\angle \mathrm{AEP}=\angle \mathrm{ADB}=90^{\circ}$
$\therefore$ By AA similarity
$\Delta \mathrm{AEP} \sim \Delta \mathrm{ADB}$
(iv) In $\Delta \mathrm{PDC}$ and $\Delta \mathrm{BEC}$,
$\angle \mathrm{PCD}=\angle \mathrm{BCE}($ common $)$
$\angle \mathrm{PDC}=\angle \mathrm{BEC}=90^{\circ}$
$\therefore$ By AA similarity
$\Delta \mathrm{PDC} \sim \Delta \mathrm{BEC}$
(i) In $\triangle \mathrm{AEP}$ and $\triangle \mathrm{CDP}$,
$\angle \mathrm{APE}=\angle \mathrm{CPD}$ (vertically opposite angles)
$\angle \mathrm{AEP}=\angle \mathrm{CDP}=90^{\circ}$
$\therefore \quad$ By AA similarity
$\Delta \mathrm{AEP} \sim \Delta \mathrm{CDP}$
(ii) In $\triangle \mathrm{ABD}$ and $\triangle \mathrm{CBE}$,
$\angle \mathrm{ABD}=\angle \mathrm{CBE}($ common $)$
$\angle \mathrm{ADB}=\angle \mathrm{CEB}=90^{\circ}$
$\therefore$ By AA similarity
$\Delta \mathrm{ABD} \sim \Delta \mathrm{CBE}$
(iii) In $\triangle \mathrm{AEP}$ and $\triangle \mathrm{ADB}$,
$\angle \mathrm{PAE}=\angle \mathrm{DAB}($ common $)$
$\angle \mathrm{AEP}=\angle \mathrm{ADB}=90^{\circ}$
$\therefore$ By AA similarity
$\Delta \mathrm{AEP} \sim \Delta \mathrm{ADB}$
(iv) In $\Delta \mathrm{PDC}$ and $\Delta \mathrm{BEC}$,
$\angle \mathrm{PCD}=\angle \mathrm{BCE}($ common $)$
$\angle \mathrm{PDC}=\angle \mathrm{BEC}=90^{\circ}$
$\therefore$ By AA similarity
$\Delta \mathrm{PDC} \sim \Delta \mathrm{BEC}$
