Question:
In figure, AOB is a diameter of the circle and C, D, E are any three points on the semi-circle. Find the value of ∠ACD + ∠BED.
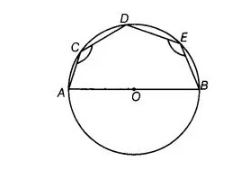
Solution:
Since, $A, C, D$ and $E$ are four point on a circle, then $A C D E$ is a cyclic quadrilateral.
$\angle A C D+\angle A E D=180^{\circ} \ldots$ (i) $\quad$ [sum of opposite angles in a cyclic quadrilateral is $180^{\circ}$ ]
Now, $\angle A E B=90^{\circ}$ ......(ii)
We know that, diameter subtends a right angle to the circle.
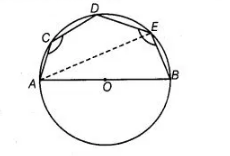
On adding Eqs. (i) and (ii), we get
$(\angle A C D+\angle A E D)+\angle A E B=180^{\circ}+90^{\circ}=270^{\circ}$
$\Rightarrow$ $\angle A C D+\angle B E D=270^{\circ}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
