Question:
In figure, $\mathrm{AT}$ is a tangent to the circle with centre 0 such that $\mathrm{OT}=4 \mathrm{~cm}$ and $\angle \mathrm{OTA}=30^{\circ}$. Then, $\mathrm{AT}$ is equal to
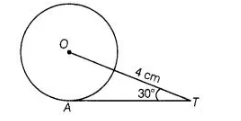
(a) 4 cm
(b) 2 cm
(c) 2√3 cm
(d) 4√3 cm
Solution:
(c) Join OA
We know that, the tangent at any point of a circle is perpendicular to the radius through the point of contact.
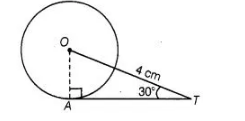
$\therefore \quad \angle O A T=90^{\circ}$
In $\triangle O A T$, $\cos 30^{\circ}=\frac{A T}{O T}$
$\Rightarrow$ $\frac{\sqrt{3}}{2}=\frac{A T}{4}$
$\Rightarrow$ $A T=2 \sqrt{3} \mathrm{~cm}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
