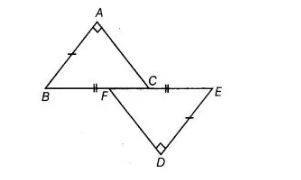
In figure, BA ⊥ AC, DE ⊥ DF

Given in figure, $B A \perp A C, D E \perp D F$ such that $B A=D E$ and $B F=E C$.

To show $\triangle A B C \cong \triangle D E F .$

Proof Since, $B F=E C$

On adding CF both sides, we get 

$B F+C F=E C+C F$

$\Rightarrow$ $B C=E F$ $\ldots(1)$ 

In $\triangle A B C$ and $\triangle D E F$, $\angle A=\angle D=90^{\circ}$ $[\because B A \perp A C$ and $D E \perp D F]$

$B C=E F$ [from Eq. (i)]

and $B A=D E$ [given]

$\therefore$ $\triangle A B C \cong \triangle D E F$ [by RHS congruence rule]