In figure, line segment DF intersects the side AC

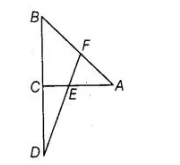
Given $\triangle A B C, E$ is the mid-point of $C A$ and $\angle A E F=\angle A F E$

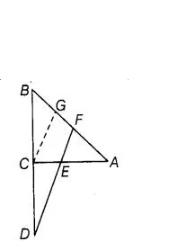
To prove $\frac{B D}{C D}=\frac{B F}{C F}$ 

Construction Take a point $G$ on $A B$ such that $C G \| E F$. Proof Since, $E$ is the mid-point of $C A$.

$\therefore$ $C E=A E$ ...(i)

In $\triangle A C G$, CG $\| E F$ and $E$ is mid-point of $C A$.

So, $C E=G F$....(ii)

[by mid-point theorem]

Now, in $\triangle B C G$ and $\triangle B D F$, $C G \| E F$

$\therefore$ $\frac{B C}{C D}=\frac{B G}{G F}$ [by basic proportionality theorem]

$\Rightarrow$ $\frac{B C}{C D}=\frac{B F-G F}{G F} \Rightarrow \frac{B C}{C D}=\frac{B F}{G F}-1$

$\Rightarrow$ $\frac{B C}{C D}+1=\frac{B F}{C E}$ [from Eq. (ii)]

$\Rightarrow$  $\frac{B C+C D}{C D}=\frac{B F}{C E} \Rightarrow \frac{B D}{C D}=\frac{B F}{C E}$ Hence proved.