Question:
In figure, O is the centre of a circle and PQ is a diameter. If
∠ROS = 40°, find ∠RTS.
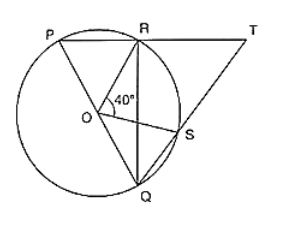
Solution:
Since PQ is diameter
Then,
∠PRQ = 90° [Angle in semicircle]
∴ ∠PRQ + ∠TRQ = 180° [Linear pair of angle]
900 + ∠TRQ = 180°
∠TRQ = 180° − 90° = 90°.
By degree measure theorem
∠ROS = 2∠RQS
⇒ 40° = 2∠RQS
⇒ ∠RQS = 40°/2 = 20°
In ΔRQT, by Angle sum property
∠RQT + ∠QRT + ∠RTS = 180°
⇒ 20° + 90° + ∠RTS = 180°
⇒ ∠RTS = 180° − 20° − 90° = 70°
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
