Question:
In figure, PQRS is a square and T and U are, respectively, the midpoints of PS and QR. Find the area of ΔOTS if PQ = 8 cm.
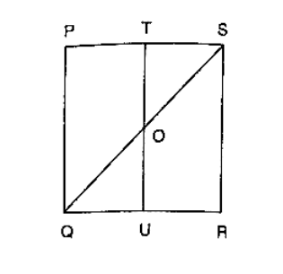
Solution:
From the figure,
T and U are mid points of PS and QR respectively
∴ TU ∥ PQ
⇒ TO ∥ PQ
Thus, in ΔPQS, T is the midpoint of PS and TO ∥ PQ
∴ TO = (1/2) PQ = 4 cm
Also, TS = (1/2) PS = 4 cm
$\therefore \operatorname{ar}(\Delta \mathrm{OTS})=(1 / 2)(\mathrm{TO} \times \mathrm{TS})=(1 / 2)(4 \times 4) \mathrm{cm}^{2}=8 \mathrm{~cm}^{2}$