In figure, X and Y are the mid points of AC and AB respectively, QP ∥ BC and CYQ and BXP are straight lines.
Question:
In figure, X and Y are the mid points of AC and AB respectively, QP ∥ BC and CYQ and BXP are straight lines. Prove that ar(ΔABP) = ar(ΔACQ).
Solution:
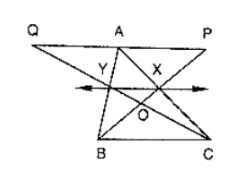
Since X and Y are the mid points of AC and AB respectively.
Therefore, XY ∥ BC
Clearly, triangles BYC and BXC are on the same base BC and between the same parallels XY and BC
∴ ar(ΔBYC) = ar(ΔBXC)
⇒ ar(ΔBYC) − ar(ΔBOC) = ar(ΔBXC) − ar(ΔBOC)
⇒ ar(ΔBOY) = ar(ΔCOX)
⇒ ar(ΔBOY) + ar(ΔXOY) = ar(ΔCOX) + ar(ΔXOY)
⇒ ar(ΔBXY) = ar(ΔCXY) .... (2)
We observed that the quadrilaterals XYAP and XYAQ are on the same base XY and between same parallels XY and PQ.
∴ ar(quad. XYAP) = ar(quad XYQA) ⋅⋅⋅⋅ (2)
Adding 1 and 2, we get
∴ ar(ΔBXY) + ar(quad. XYAP) = ar(ΔCXY) + ar(quad XYQA)
⇒ ar(ΔABP) = ar(ΔACQ)