In given figure, if ∠A = ∠C, AB = 6 cm,

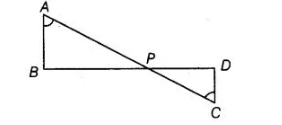
Given,∠A = ∠C, AS = 6cm, BP = 15cm, AP = 12 cm and CP = 4cm

In ΔAPB and ΔCPD,                       ∠A =∠C                                                                    [given]

∠APS = ∠CPD                              [vertically opposite angles]

$\therefore \quad \Delta A P D \sim \triangle C P D$

$\Rightarrow \quad \frac{A P}{C P}=\frac{P B}{P D}=\frac{A B}{C D}$

$\Rightarrow \quad \frac{12}{4}=\frac{15}{P D}=\frac{6}{C D}$

On taking first two terms, we get

$\frac{12}{4}=\frac{15}{P D}$

$\Rightarrow \quad P D=\frac{15 \times 4}{12}=5 \mathrm{~cm}$

On taking first and last term, we get

$\frac{12}{4}=\frac{6}{C D}$

$\Rightarrow$ $C D=\frac{6 \times 4}{12}=2 \mathrm{~cm}$

Hence, length of PD = 5 cm and length of CD = 2 cm