In how many ways can 5 boys and 3 girls be seated in a row so

Given: We have 5 boys and 3 girls

To Find: Number of ways of seating so that 5 boys and 3 girls are seated in a row and each girl is between 2 boys

The formula used: The number of permutations of n different objects taken r at a time

(object does not repeat) is ${ }^{n} P_{r}=\frac{n !}{(n-r) !}$

The only arrangement possible is

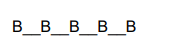
Number of ways for boys $={ }^{n} P_{r}$

$={ }^{5} P_{5}$

$=\frac{5 !}{(5-5) !}$

$=\frac{5 !}{0 !}$

=120

There are 3 girls, and they have 4 vacant positions

Number of ways for girls $={ }^{4} P_{3}=24$ ways

$=\frac{4 !}{(4-3) !}$

$=\frac{4 !}{1 !}$

$=24$

Total number of ways $=24 \times 120=2880$

In 2880 ways 5 boys and 3 girls can be seated in a row so that each girl is between 2 boys.