Question:
In how many ways can the letters of the word ‘INTERMEDIATE’ be arranged so that:
(i) The vowels always occupy even places?
(ii) The relative orders of vowels and consonants do not change?
Solution:
(i)
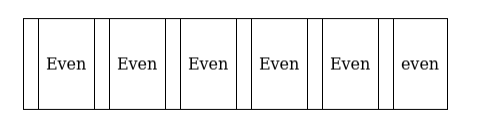
There are 6 even places and 6 vowels out of which 2 are of 1 kind, 3 are of the $2^{\text {nd }}$ kind
The vowels can be arranged in $\frac{6 !}{2 ! 3 !}=60$
There are 6 consonants out of which 2 is of one kind
Number of permutations $=\frac{6 !}{2 !}=360$
$\Rightarrow$ Total number of words $=360 \times 60=21600$
(ii)
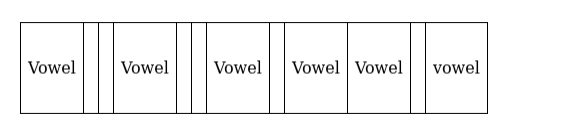
There are 6 vowels to arrange in $\frac{6 !}{2 ! 3 !}$
There are 6 consonants which can be arranged in $\frac{6 !}{2 !}$
$\Rightarrow$ Total number of ways $=\frac{6 !}{2 ! 3 !} \times \frac{6 !}{2 !}=21600$