In right-angled triangle ABC is which ∠C = 90°,

$\triangle \mathrm{ABC}$ is a right-angled triangle with $\angle \mathrm{C}=90^{\circ}$. D is the mid-point of $\mathrm{BC}$.

We need to prove that $A B^{2}=4 A D^{2}-3 A C^{2}$.

Join AD.

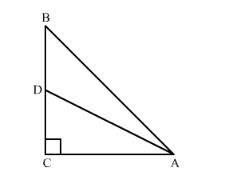
Since D is the midpoint of the side BC, we get

BD = DC

$\therefore B C=2 D C$

Using Pythagoras theorem in triangles right angled triangle ABC

$A B^{2}=A C^{2}+B C^{2}$

$A B^{2}=A C^{2}+(2 D C)^{2}$

$A B^{2}=A C^{2}+4 D C^{2}$

Again using Pythagoras theorem in the right angled triangle ADC

$A D^{2}=A C^{2}+D C^{2}$

$D C^{2}=A D^{2}-A C^{2}$....(2)

From (1) and (2), we get

$A B^{2}=A C^{2}+4\left(A D^{2}-A C^{2}\right)$

$A B^{2}=A C^{2}+4 A D^{2}-4 A C^{2}$

$A B^{2}=4 A D^{2}-3 A C^{2}$

Hence, $A B^{2}=4 A D^{2}-3 A C^{2}$.