Question:
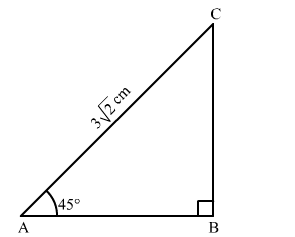
In the adjoining figure, $\triangle A B C$ is a right-angled at $B$ and $\angle A=45^{\circ}$. If $A C=3 \sqrt{2} \mathrm{~cm}$,
find
(i) BC,
(ii) AB.
Solution:
From right-angled ∆ABC, we have:
$\frac{B C}{A C}=\sin 45^{\circ}$
$\Rightarrow \frac{B C}{3 \sqrt{2}}=\frac{1}{\sqrt{2}} \Rightarrow B C=3 \mathrm{~cm}$
Also, $\frac{A B}{A C}=\cos 45^{\circ}$
$\Rightarrow \frac{A B}{3 \sqrt{2}}=\frac{1}{\sqrt{2}} \Rightarrow A B=3 \mathrm{~cm}$
$\therefore B C=3 \mathrm{~cm}$ and $A B=3 \mathrm{~cm}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
