Question:
In the adjoining figure, ABCD is a trapezium in which AB || DC; AB = 7 cm; AD = BC = 5 cm and the distance between AB and DC is 4 cm. Find the length of DC and hence, find the area of trap. ABCD.
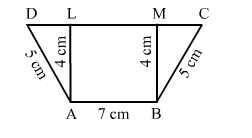
Solution:
∆ADL is a right angle triangle.
So, $D L=\sqrt{\left(5^{2}-4^{2}\right)}=\sqrt{9}=3 \mathrm{~cm}$
Similarly, in ∆BMC, we have:
$M C=\sqrt{\left(5^{2}-4^{2}\right)}=\sqrt{9}=3 \mathrm{~cm}$
∴ DC = DL + LM + MC = 3 + 7 + 3 = 13 cm
Now, ar(trapezium. $A B C D)=\frac{1}{2} \times($ sum of parallel sides $) \times($ distance between them $)$
$=\frac{1}{2} \times(7+13) \times 4$
$=40 \mathrm{~cm}^{2}$
Hence, $D C=13 \mathrm{~cm}$ and area of trapezium $=40 \mathrm{~cm}^{2}$
