In the adjoining figure, ABCD is a trapezium in which AB || DC and its diagonals AC and BD intersect at O.
Question:
In the adjoining figure, ABCD is a trapezium in which AB || DC and its diagonals AC and BD intersect at O. Prove that ar(∆AOD) = ar(∆BOC).
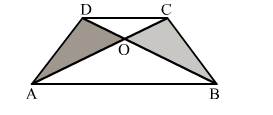
Solution:
∆CDA and ∆CBD lies on the same base and between the same parallel lines.
So, ar(∆CDA) = ar(CDB) ...(i)
Subtracting ar(∆OCD) from both sides of equation (i), we get:
ar(∆CDA)
⇒ ar(∆AOD) = ar(∆BOC)
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.