Question:
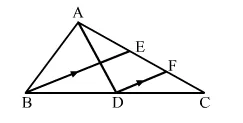
In the adjoining figure, $A D$ and $B E$ are the medians of $\triangle A B C$ and $D F \| B E$. Show that $C F=\frac{1}{4} A C$.
Solution:
In ∆ABC, we have:
AC = AE + EC ...(i)
AE = EC ...(ii) [BE is the median of ∆ABC]
∴ AC = 2EC ...(iii)
In ∆BEC, DF || BE.
∴ EF = CF (By midpoint theorem, as D is the midpoint of BC)
But EC = EF + CF
⇒ EC = 2 ⨯ CF ...(iv)
From (iii) and (iv), we get:
AC = 2 ⨯ (2 ⨯ CF)
$\therefore C F=\frac{1}{4} A C$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.