Question:
In the adjoining figure, DE || BC. Prove that
(i) ar(∆ACD) = ar(∆ABE),
(ii) ar(∆OCE) = ar(∆OBD),
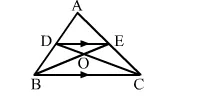
Solution:
∆DEC and ∆DEB lies on the same base and between the same parallel lines.
So, ar(∆DEC) = ar(∆DEB) ...(1)
(i) On adding ar(∆ADE) in both sides of equation (1), we get:
ar(∆DEC) + ar(∆ADE) = ar(∆DEB) + ar(∆ADE)
⇒ ar(∆ACD) = ar(∆ABE)
(ii) On subtracting ar(ODE) from both sides of equation (1), we get:
ar(∆DEC)
⇒ ar(∆OCE) = ar(∆OBD)
